k-mooc 으로 선형대수학 독학하기 !
강의 내용 : 선형대수학
출처 : 성균관대학교 이상구 교수님
* 원래 강의는 sage를 이용하는데 중간부터 나는 R을 사용하는 것으로 변경함.
1~2강에서 전체적인 내용을 간략히 배우고
3강부터 상세하게 배우는 듯
[k-mooc] 3.2 행렬대수_역행렬
아직까진 할만하다 홧팅~~.~ [kmooc] 03-1 행렬대수 - 행렬연산 앞으로 한 번에 안올리고 나눠서 올려야겠다 ^o^~ 계속 스크롤 내려서 작성하려니 힘들어서 그냥 하나 하고 올리는 걸로 변경 ㅎㅎ [k-mo
nyoungsom.tistory.com
3.3 기본행렬(elementary matrix)
기본행렬(elementary matrix), 치환행렬(permutation matrix)
* 기본행렬(elementary matrices)은
* 치환행렬(permutation mtarix)은
[R 실습] 기본행렬
* 기본행렬
* 두 행을 교환함.
* 기본행렬의 2행인
* 한 행에 영이 아닌 상수배를 해서 다른 행에 더함.
* 기본행렬의 1행에 2를 곱한 값은 2행에 더함.
* 한 행에 영이 아닌 상수배를 함.
* 기본행렬의 2행에 3을 곱함.
a <- c(1,0,0,0,1,0,0,0,1)
A = matrix(a,3,3,T) # 원소 a, 3행, 3열, 순서대로
B <- A
B[B[2,] <- A[3,], B[3,] <- A[2,]]
B <- A
B[2,] <- A[2,]+A[1,]*2
B <- A
B[2,] <- B[2,]*3
기본행렬의 역행렬
기본행렬의 역행렬 또한 기본행렬임.
1)

2)

3)

a <- c(1,0,0,0,1,0,0,0,1)
A = matrix(a,3,3,T)
solve(A)
b <- c(1,0,0,0,0,1,0,1,0) # 1
B = matrix(b,3,3,T)
solve(B)
c <- c(1,0,0,0,2,0,0,0,1) # 2
C = matrix(c,3,3,T)
solve(C)
d <- c(1,0,0,0,1,0,0,2,1) # 3
D = matrix(d,3,3,T)
solve(D)

1)

2)

3)

가역행렬과 동치인 명제
임의의
1)
2)
3)
4)
기본행연산
*
* 기본행연산(ERO)을 유한히 반복함으로써, 단위행렬을 만들 수 있음.
*
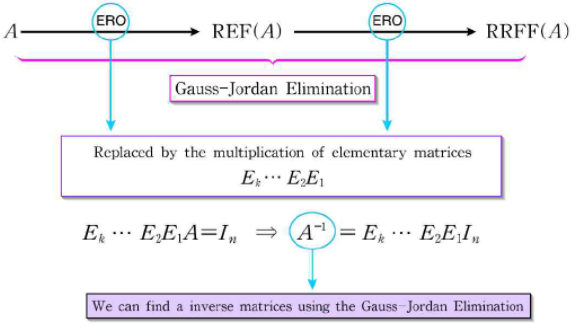
기본행렬로 역행렬 구하기
1)
주어진 행렬
2) 단계 1에서 만든 행렬
3) 단계 2에서 얻은 RREF를
*
*
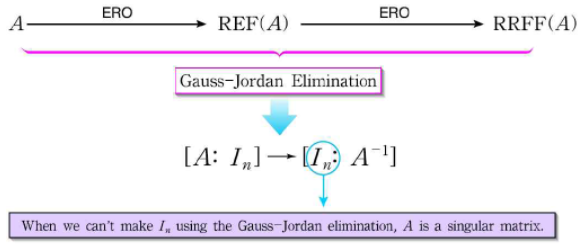
[R 실습] 기본행렬로 역행렬 구하기 1
Q)

A)
1)

2)

3)
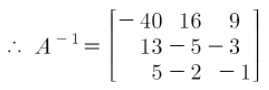
a <- c(1,2,3,2,5,3,1,0,8)
A = matrix(a,3,3,T)
solve(A)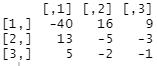
[R 실습] 기본행렬로 역행렬 구하기 2
Q)

A)
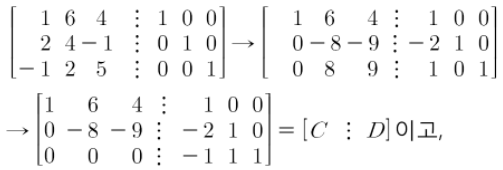

[R 실습] 기본행렬로 역행렬 구하기 3
Q)

A)
library(MASS)
a <- c(1,-1,2,-1,0,2,-6,4,11)
A = matrix(a,3,3,T)
solve(A)
fractions(solve(A))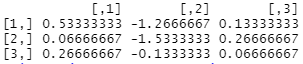
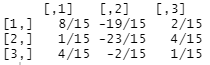
'녕's Study > 선형대수학' 카테고리의 다른 글
| [k-mooc] 3.4 부분공간과 일차독립 (0) | 2022.02.09 |
|---|---|
| [k-mooc] 3.2 행렬대수_역행렬 (0) | 2022.01.17 |
| [kmooc] 3.1 행렬대수 - 행렬연산 (0) | 2022.01.14 |
| [k-mooc] 2 선형연립방정식 (0) | 2022.01.05 |
| [k-mooc] 1 벡터 (0) | 2021.12.31 |




