k-mooc 으로 선형대수학 독학하기 !
강의 내용 : 선형대수학
출처 : 성균관대학교 이상구 교수님
* 원래 강의는 sage를 이용하는데 중간부터 나는 R을 사용하는 것으로 변경함.
01 벡터
선형대수학은 "벡터(vector)", "행렬(matrix)"를 대상으로 연구함. 1.1 공학과 수학에서의 벡터 1.2 내적과 직교 1.3 직선과 평면의 벡터 방정식 1.1 공학과 수학에서의 벡터 물리학에서 벡터 운동법칙,
nyoungsom.tistory.com
2.1 선형연립방정식
2.2 Gauss 소거법과 Gauss-Jordan 소거법
2.3 선형연립방정식의 응용
2.1 선형연립방정식
선형방정식(linear equation)
\( a_1 x_1 + a_2 x_2 + ... + a_n x_n = b \)
* 차수가 1인 미지수의 일차식과 상수항으로 이루어진 방정식
* \(b \)와 \( a_1, a_2, ... , a_n \)이 실수일 때, 미지수 \( x_1, x_2, ... , x_n \)에 관한 선형방정식
선형방적식의 예
* 1)의 방정식은 2)로 정리할 수 있으며, 선형방정식임.

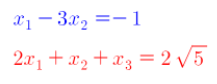
* 3)은 선형방정식이 아님.

선형연립방정식(system of linear equations)
* 미지수 \( x_1, x_2, ... , x_n \)에 관한 유한개의 선형방정식들의 모임을 선형연립방정식이라 함.
* 상수항 \( b_1, b_2, ... , b_n \)이 모두 0일 경우, 동차선형연립방정식(동차선형방정식시스템, homogeneous system of linear equation)이라 함.
\( \begin{align} & a_11 x_1 + a_12 x_2 + \cdots + a_1n x_n = b_1 \\ & a_21 x_21 + a_22 x_22 + \cdots + a_2n x_2n = b_2 \\ & \vdots \\ & a_m1 x_m1 + a_m2 x_m2 + \cdots + a_mn x_mn = b_m \end{align} \)
선형연립방정식의 해(solution)
* 선형연립방정식의 미지수 \( ( x_1, x_2, \cdots , x_n ) \)에 어떤 수 \( ( s_1, s_2, \cdots , s_n ) \)을 각각 대입했을 때, 각 방정식이 모두 성립하면 어떤 수 \( ( s_1, s_2, \cdots , s_n ) \)를 선형연립방정식의 해라고 함.
* 해가 존재하는 경우는 consitent라고 하며, 반면에 해가 존재하지 않는 경우는 inconsistent라고 함.
* 선형연립방정식의 해 전체의 집합을 선형연립방정식의 해집합(solution set)이라 함.
* 동일한 해집합을 가지는 두 선형연립방정식을 동차(equivalent)라고 함.
해집합(미지수가 2개인 선형연립방정식)
* 선형연립방정식에 대하여 다음 중 하나가 성립함.
1) 유일한 해를 가짐.
2) 해를 갖지 않음.
3) 무수히 많은 해를 가짐.
\( \begin{align} & x_1 + x_2 = 3 \\ & x_1 - x_2 = 1 \end{align} \)

\( \begin{align} & 2x_1 - x_2 = -2 \\ & -2x_2 + x_2 = 4 \end{align} \)

\( \begin{align} & 2x_1 - x_2 = -2 \\ & -2x_1 + x_2 = 2 \end{align} \)

선형연립방정식 풀이
Q)
\( \begin{align} x_1 - 2x_2 + x_3 + 3x_4 - x_5 = 0 & \\ x_3 - 5x_4 + 2x_5 = 1 & \\ x_4 + x_5 = 2 \end{align} \)
A)
\( S = \left\{ \left( x_1, x_2, x_3, x_4, x_5 \right) = \left( -17 + 2s + 11t, s, 11-7t, 2-t, t \right) \mid s,t \in R \right\} \)
계수행렬(coefficient matrix), 첨가행렬(augmented matrix)
\( \begin{align} & a_11 x_1 + a_12 x_2 + \cdots + a_1n x_n = b_1 \\ & a_21 x_1 + a_22 x_2 + \cdots + a_2n x_n = b_2 \\ \vdots \\ & a_m1 x_1 + a_m2 x_2 + \cdots + a_mn x_n = b_m \end{align} \)
* n개의 미지수를 갖는 m개의 일차방정식으로 이루어진 선형연립방정식
\( Ax = b \)

* 행렬 A는 선형연립방정식의 계수행렬

* A에 b를 붙여서 만든 행렬로 선형연립방정식의 첨가행렬
[실습] 계수행렬과 첨가행렬 풀이
Q) 선형연립방정식을 행렬의 곱으로 나타내고 첨가행렬을 구하라.
\( \begin{align} x + y + 2z = 9 \\ 2x + 4y - 3z = 1 \\ 3x + 6y - 5z = 0 \end{align} \)
A) 계수행렬 A, 미지수 x, 상수항 b



A=matrix(3, 3, [1,1,2,2,4,-3,3,6,-5]) # 3x3 행렬 입력
b=vector([9,1,0]) # 상수항 벡터 입력
print A.augment(b) # 첨가행렬
2.2 Gauss 소거법과 Gauss-Jordan 소거법
선형연립방정식의 풀이(소거법)

* 선형연립방정식의 해집합을 바꾸지 않는다.
* 기본행 연산
1) 두 식을 교환
2) 한 식에 0 아닌 실수를 곱합
3) 한 식에 0 아닌 실수배를 하여 다른 식에 더함.
선형연립방정식의 풀이
\( \begin{align} x + y + 2z = 9 \qquad (1) R_1 \\ 2x + 4y - 3z = 1 \qquad (2) R_2 \\ 3x + 6y -5z = 0 \qquad (3) R_3 \end{align} \)

* 왼쪽 : 연립방정식 풀이 과정 / 오른쪽 : 연립방정식의 첨가행렬 변화

* \( (1) \times 2 \)를 \( (2) \)에 더함.

* \( (2) \times -3 )\을 \( (3) \)에 더함

* \( (3) \times \frac{1}{2} \)

* \( (2) \times -3 \)을 \( (3) \)에 더함

* \( (3) \times -2 \)
\( \begin{align} & z = 3 \\ & y = \frac{7}{2}z - \frac{17}{2} = 2 \\ & x = 9 - y - 2z = 1 \end{align} \)
\( \therefore x=1, y=2, z=3 \)
행 사다리꼴(REF, row echelon form), 기약 행 사다리꼴(RREF, reduced row echelon form)
* 행 사다리꼴의 조건, \( m \times n \) 행렬 \( E \)가 다음을 만족함.
- 성분이 모두 0인 행이 존재하면 그 행은 행렬의 맨 아래에 위치함.
- 각 행에서 처음으로 나타나는 0이 아닌 성분은 1임.
이 때, 1을 그 행의 선행성분(leading entry)라고 함. - \( i \)행과 \( (i + 1) \)행 모두에 선행성분이 존재하면,
\( (i+1) \)행의 선행선분은 \( i \)행의 선행성분보다 오른쪽에 위치함.
* 기약 행 사다리꼴 조건, 행렬 \( E \)가 행 사다리꼴이고 다음을 만족함.
- 어떤 행의 선행성분을 포함하는 열의 다른 성분은 모두 0임.
행 사다리꼴(REF)

행 사다리꼴(REF)이 아닌 경우

기약 행 사다리꼴(RREF)

행 사다리꼴(REF), 기약 행 사다리꼴(RREF)
(*은 임의의 수)

기본행 연산(ERO, Elementary Row Operation)
* \( m \times n \) 행렬 A에 관한 연산으로 REF와 RREF로 바꾸는 연산임.
\( R_i \leftrightarrow R_j \)
* E1 : A의 두 행 i행과 j행을 서로 바꿈
\( kR_j \)
* E2 : A의 i행에 0이 아닌 상수 k를 곱함
\( kR_i + R_j \)
* A의 i행을 k배 하여 j행에 더함
행동치(row equivalent)
* 행렬 A에 기본행 연산을 시행하여 얻어지는 행렬이 B일 때, A와 B는 행동치임
* 첨가행렬이 행동치인 두 연립방정식의 해집합은 같음

REF와 RREF 만들기


* 1) 모든 성분이 0이 아닌 열 중에 가장 좌측열을 찾음.
* 이 행렬의 경우는 첫번 째 열임
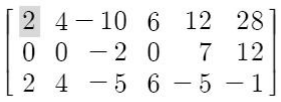
* 가장 위에 있는 성분이 0일 때, 그 열의 위에서부터 처음으로 0이 아닌 성분을 포함하는 행과 한 행을 교환함.
* (가능하면 1, -1 또는 2 등의 성분을 취함.)
* 이 행렬의 경우는 1열의 2행 성분이 대상임.
* 2) 1행과 2행을 교환함

* 1행의 선행성분을 1로 만들어야 함
* 3) 1행을 2로 나눔

* 1행의 선행선분 아래에 있는 모든 성분을 0으로 만듬(행연산)
* 4) 1행을 -2배한 값을 3행에 더함



* 1행을 제외하고 성분 모두가 0이아닌 열을 찾아 과정을 반복함
* 5) 1행 제외하고 성분 모두가 0이 아닌 열에 3~4)를 시행


* 5) 1,2행 제외하고 성분 모두가 0이 아닌 열에 3~4)를 시행

* REF

* 3행에 7/2를 곱한 값을 2행에 더함

* 3행에 -6을 곱한 값을 1행에 더함

* 2행에 5를 곱한값을 1행에 더함
*RREF
* 행렬의 크기가 3차 이상인 경우 손으로 해결하기 까다로우므로 통계패키지를 사용함.
[R 실습] RREF 풀이
* 행렬 \( A \)의 RREF를 구하라

n <- c(1,1,1,4,4,2,3,4,9,16,-2,0,3,-7,11)
A <- matrix(n, nrow=3, ncol=5, byrow=T) # byrow=T : 순차적으로 행렬 넣기
#install.packages('matlib')
library('matlib')
echelon(A, verbose=TRUE, fractions=TRUE)
행동치
* 첨가행렬이 행동치인 두 선형연립방정식은 동치임
* (즉, 해집합이 같다.)
[R 실습] Gauss 소거법 풀이
* 선형연립방정식의 첨가행렬을 REF로 변형하여 푸는 방법
\( \begin{align} & x + 2y + 3x = 9 \\ & 2x - y + z = 8 \\ & 3x \qquad -z = 3 \end{align} \)
a <- matrix(c(1,2,3,2,-1,1,3,0,-1), ncol=3, nrow=3, byrow=T)
b <- matrix(c(9,8,3), ncol=1, byrow=T)
det(a) # 행렬식(determinant)
solve(a,b)
echelon(a, b, reduced=FALSE, verbose=TRUE, fractions=TRUE) # row-echelon form
echelon(a, b) # solving the matrix equation Ax = b
echelon(a, diag(3)) # inverting A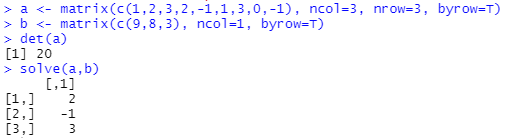
\( x=2, y=-1, z=3 \)
[R 실습] Gauss-Jordan 소거법 풀이
* 선형연립방정식의 첨가행렬을 RREF로 변형하여 푸는 방법
\( \begin{align} x_1 + 3x_2 -2x_3 + \qquad 2x_5 \qquad = 0 & \\ 2x_1 + 6x_2 -5x_3 -2x_4 + 4x_5 - 3x_6 = -1 & \\ \qquad \qquad 5x_3 + 10x_4 \qquad +15x_6 = 5 & \\ 2x_1 + 6x_2 \qquad + 8x_4 + 4x_5 + 18x_6 = 6 \end{align} \)
n2 <- c(1,3,-2,0,2,0,2,6,-5,-2,4,-3,0,0,5,10,0,15,2,6,0,8,4,18)
a2 = matrix(n2, ncol=6, nrow=4, byrow=T)
b2 = matrix(c(0,-1,5,6), nrow=4)
A2 <- echelon(a2,b2, verbose=TRUE, fractions=TRUE) # reduced row-echelon form
echelon(a3, b3) # solving the matrix equation Ax = b
echelon(a3, diag(4)) # inverting A

\( x_1 = -3r-4s-2t, \ x_2 = r, \ x_3 = -2s, \ x_4 = s, \ x_5 = t, \ x_6 = \frac{1}{3} \)
* 일반 해

* 벡터 형식의 해
Gauss 소거법과 Gauss-Jordan 소거법

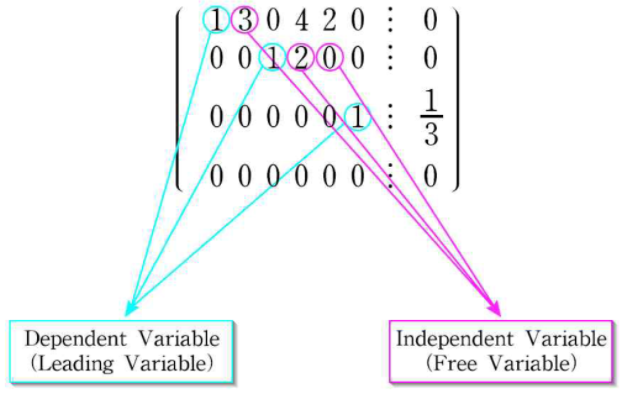
선형변수, 자유변수와 RREF의 관계
* 자유변수(독립변수, Independet Variable)는 첨가행렬의 RREF중 선행성분 1을 포함하지 않는 열에 대응하는 변수
* 선행변수(종속변수, Dependent Variable)는 선행선분 1을 포함하는 열에 대응하는 변수
동차(homogeneous)연립방정식
* 동차 연립방정식은 \( x = 0 \)을 유일한 해(trivial solution)으로 갖는 경우와 무수히 많은 해를 갖는 두가지 경우만 있음.

Gauss-Jordan 소거법 풀이2
\( \begin{align} x_1 + 3x_2 - 2x_3 \qquad + 2x_5 + \qquad = 0 & \\ 2x_1 + 6x_2 - 5x_3 - 2x_4 + 4x_5 - 3x_6 = 0 & \\ \qquad \qquad 5x_3 + 10x_4 \qquad + 15x_6 = 0 & \\ 2x_1 + 6x_2 \qquad + 8x_4 + 4x_5 + 18x_6 = 0 \end{align} \)
n3 <- c(1,3,-2,0,2,0,
2,6,-5,-2,4,-3,
0,0,5,10,0,15,2,
6,0,8,4,18)
a3 = matrix(n3, ncol=6, nrow=4, byrow=T)
b3 = matrix(c(0,0,0,0), nrow=4)
A3 <- echelon(a3, b3, verbose=TRUE, fractions=TRUE) # reduced row-echelon form
echelon(a3, b3) # solving the matrix equation Ax = b
echelon(a3, diag(4)) # inverting A
\( x_1 = -3r-4s-2t, \ x2=r, \ x_3=-2s, \ x_4=s, \ x_5=t, \ x_6=0 \)
* 일반해
* 자유변수를 각각 \(x_2 = r, \ x_4 = s, \ x_5 = t \)로 지정

* 벡터해
동차연립방정식의 자유변수 개수정리
* \( n \)개의 미지수를 갖는 동차연립방정식에 대하여 첨가행렬의 RREF가 \( r \)개의 선행성분 1(leading 1)을 갖는다면
해집합은 \( n-r \)개의 자유변수를 갖는다.
2.3 선형연립방정식의 응용
[R 실습] 전자회로 문제
* 전류 \( I_i \)를 구하는 연립방정식을 구하라
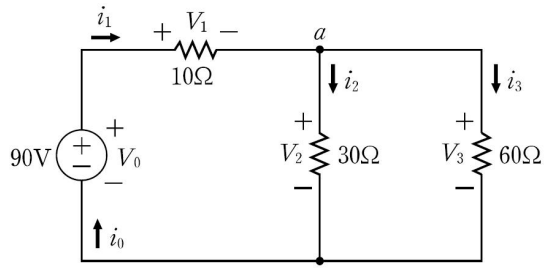
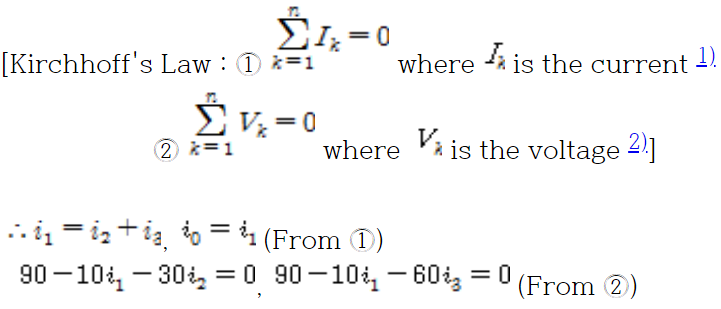
\( \therefore \begin{align} i_0 - i_1 \qquad \qquad = 0 & \\ \qquad i_1 -i_2 -i_3 = 0 & \\ \qquad i_1 + 3i_2 \qquad = 9 & \\ \qquad i_1 \qquad + 6i_3 = 9 \end{align} \)
* 전하량보존의 법칙
* 옴의 법칙 : \( V = IR \)

n4 <- c(1,-1,0,0,
1,0,-1,-1,
0,1,3,0,
0,0,1,-2)
a4 = matrix(n4, ncol=4, nrow=4, byrow=T)
b4 = matrix(c(0,0,9,0), nrow=4)
echelon(a4, b4, verbose=TRUE, fractions=TRUE) # reduced row-echelon form
echelon(a4, diag(4)) # inverting A
CT촬영 문제
* X-ray 촬영 : 2D 이미지
* CT 촬영 : 3D 이미지
Q) 이 CT는 X선을 체내에 통과시킨 후 X선의 양을 측정함. 그리고 각 신체 부위에서 흡수된 X선의 양을 계산 및 합성하여 신체 내부의 입체 영상을 볼 수 있게 해주는 장치임. 다음 그림처럼 투사한 X선의 양을 10이라 할 때, 투과되어 나온 X선의 양을 측정하라.
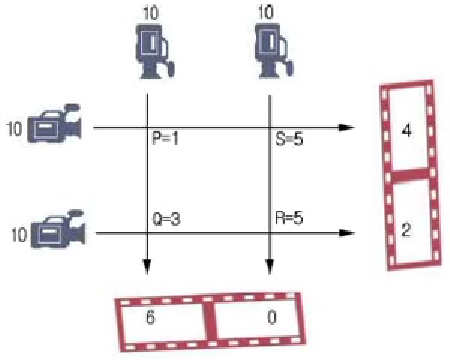
comment > 다음 풀이처럼 하려면, 각 미지수의 값을 알고 있어야 하는데 그림에서 출력값이 잘못된건지..? 🤔
A)
\( \begin{align} P + S \qquad \qquad = 6, & \\ \qquad \qquad Q + R = 8, & \\ P \qquad + Q \qquad =4, & \\ \qquad S + \qquad R = 10 \end{align} \)
* \( P, Q, R, S \)의 각 지점에서 흡수된 양을 계산할 수 있음.
즉, \( P \)와 \( S \)는 6, \( Q \)와 \( S \)는 4, \( P \)와 \( Q \)는 10만큼 각각 흡수하였음.
\( \therefore P=1, \ Q=3, \ R=5, \ S=5 \)
* 따라서, 각 부위에서 흡수한 양을 측정할 수 있으므로 이를 합성하면 영상을 볼 수 있음.
* 가로 100, 세로100 군데에서 X선을 쏜다면 미지수가 \( 100 \times 100 \) (개)이고 이를 연립방정식으로 풀면 흡수된 방사능의 양윽 측정할 수 있음. 이를 통해 좀 더 정밀한 영상을 얻을 수 있음.
화학반응식의 균형 문제
Q) 다음 화학반응식을 화학균형식으로 만들어라.
\( C_2 H_6 + O_2 \rightarrow CO_2 + H_2 O \)
A)
\( x_1 C_2 H_6 + x_2 O_2 \rightarrow x_3 CO_2 + x_4 H_2 O \)
\( \begin{align} & 탄소(C) : 2x_1 = x_3 \\ & 수소(H) : 6x_1 = 2x_4 \\ & 산소(O) : 2x_2 = 2x_3 + x_4 \end{align} \)
* 각 원소의 원자 수는 서로 같음.
\( \begin{align} 2x_1 \qquad - x_3 \qquad = 0 \\ 6x_1 \qquad \qquad - 2x_4 = 0 \\ \qquad 2x_2 - 2x_3 -x_4 = 0 \end{align} \)
* 연립방정식
# library('matlib') # could not find function "echelon" 에러시, 주석풀고 라이브러리 임포트 하기
n <- c(2,0,-1,0,
6,0,0,-2,
0,2,-2,-1)
a = matrix(n, ncol=4, nrow=3, byrow=T)
echelon(a, verbose=TRUE, fractions=TRUE) # reduced row-echelon form
\( x_1 =\frac{1}{3} t, \ x_2 = \frac{7}{6} t , \ x_3 = \frac{2}{3} t , \ x_4 = t \)
* 미지수 \(x_4 \)의 값을 임의의 실수 \( t \)라고 설정함.
\( \therefore \ x_1 = 2, \ x_2 = 7, \ x_3 = 4, \ x_4 = 6 \)
* 분모를 없애기 위해 임의의 실수 \( t \)에 6을 대입해 봄.
\( 2C_2 H_6 + 7O_2 \rightarrow 4CO_2 + 6H_2O \)
[R 실습] 소행성의 궤도 문제
Q) 어떤 소행성의 궤도를 구하기 위해, 태양을 원점으로 갖는 좌표평면을 설정하였다. 축의 눈금 단위들은 측정단위(천문학 단위)가 사용된다. 행성은 타원형 궤도를 따라 운행한다(캐플러의 제1법칙). 타원 방정식의 일반형은 다음과 같다.
\( ax^2 + bxy + cy^2 + dx + ey + f = 0 \)
\( a=1 \)이라 가정할 때, \( b,c,d,e,f \)를 결정할 수 있다면 그 행성의 궤도는 완전히 결정된다. 다섯개의 관측점이 필요하므로 천문학자는 다섯번에 걸쳐 행성의 위치를 나타내는 다음 점들을 얻었다고 가정하자. 이를 타원방정식에 대입하여 연립방정식을 풀고 그 해를 찾아라.
| \( x \) | 8.025 | 10.170 | 11.202 | 10.736 | 9.092 |
| \( y \) | 8.310 | 6.355 | 3.212 | 0.375 | -2.267 |
A)
#install.packages('matlib')
library('matlib')
x <- c(8.025, 10.170, 11.202, 10.736, 9.092)
y <- c(8.310, 6.355, 3.212, 0.375, -2.267)
n <- c(x^2, x*y, y^2, x, y)
#C <- A%*%B # 행렬의 곱
A <- t(matrix(n, ncol=5, nrow=5, byrow=T))
A2 <- cbind(A, c(1,1,1,1,1))
# rownames(A) <- LETTERS[1:5]
colnames(A2) <- paste("X", 1:6, sep="")
b <- matrix(-A2[,1], ncol=1, byrow=T)
colnames(b) <- paste("X", 1, sep="")
A2b <- echelon(A2[,c(2,3,4,5,6)],b,verbose=TRUE, fractions=TRUE) # reduced row-echelon form
# a[nrow(a)-1:nrow(a), ncol(a)-1:ncol(a)]
z <- A2b[,6]
#install.packages('PlaneGeometry')
library(PlaneGeometry)
ell <- EllipseFromEquation(A = 1, B = z[1], C = z[2],D = z[3], E = z[4], F= z[5])
box <- ell$boundingbox()
plot(NULL, asp = 1, xlim = box$x, ylim = box$y, xlab = NA, ylab = NA)
draw(ell, col = "white", border = "black", lwd = 2)
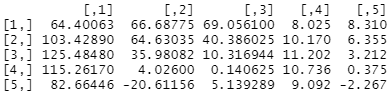
* \( x, y \)를 대입한 연립방정식의 행렬

* \( a=1 \)을 가정하므로 마지막 열로 순서를 변경하여 \( RREF \)를 구함.
Comment > \( a=1 \)이므로 미지수가 없는 상수항이라고 판명되어 반대편으로 넘기면서 마이너스로 된 듯?
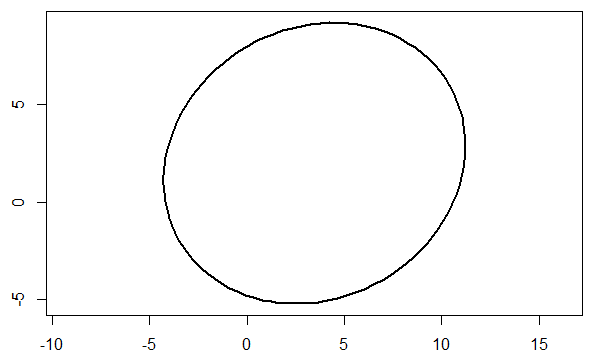
* 소행성의 궤도
# install.packages('plot3D')
library("plot3D")
# Create a scatter plot
scatter3D(x ,y ,z, phi = 0, bty = "g",
pch = 20, cex = 2, ticktype = "detailed")
# Add another point (black color)
scatter3D(x=8.025,y=8.310,z=0.02260763, add = TRUE, colkey = FALSE,
pch = 18, cex = 3, col = "black")
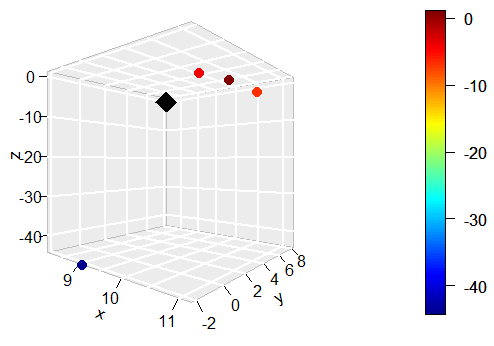
* Comment > 맞는진 모르겠지만 그냥 해 봄
[R 실습] 중심가 내 자동차의 분당 평균수 문제
Q) 각 거리가 일방통행이며, 표기된 숫자는 오후 3:30분 경 해당 거리를 집입하거나 벗어나는 자동차의 분당 평균수임.
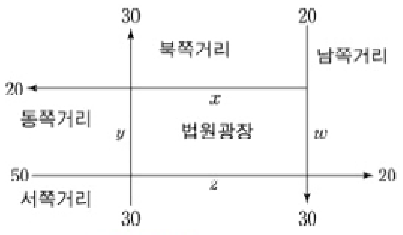
교차로를 진입하는 자동차의 총수와 벗어나는 자동차의 총수가 같을 때, 동쪽거리와 북쪽거리의 교차로로부터 \( x + t = 50 \)을 얻을 수 있음. 이와 같은 방식으로 일차방정식을 구하면 다음과 같음.
\( \begin{align} x+ y \qquad \qquad = 50 & \\ \qquad y + z \qquad = 80 & \\ \qquad \qquad z + w = 50 & \\ x \qquad \qquad + w = 20 \end{align} \)
A)
num <- matrix(c(1,1,0,0,
0,1,1,0,
0,0,1,1,
1,0,0,1), ncol=4, nrow=4, byrow=T)
total = matrix(c(50,80,50,20), ncol=1, byrow=T)
echelon(num,total, reduced=FALSE, verbose=TRUE, fractions=TRUE) # row-echelon form* Gauss 소거법

\( \therefore w = t, \ z = 50-t, \ y = 30 - t, \ x = 20-t \)
* \( t \)는 교통량이므로 \( 0 \le t \le 20 \)
\( \therefore 0 \le x \le 20, 30 \le y \le 50, 30 \le z \le 50, 0 \le w \le 20 \)
방데르몽드 행렬(Vandermonde matrix)
* 선형연립방정식은 주어진 점을 지나가는 다항식 문제(interpolation)에도 활용되어짐.
* Vandermonde 행렬을 이용한 Gauss-Jordan 소거법을 통해 얻을 수 있음.
* Vandermonde 행렬은 각 행의 첫 성분이 1인 행렬로 \( V_{ij} = \alpha_i^{i-j} \)
* 강의에 추가 설명 있음.

vandermonde.matrix function - RDocumentation
The column dimension of the Vandermonde matrix
www.rdocumentation.org
echelon function - RDocumentation
When the matrix A is square and non-singular, the reduced row-echelon result will be the identity matrix, while the row-echelon from will be an upper triangle matrix. Otherwise, the result will have some all-zero rows, and the rank of the matrix is the num
www.rdocumentation.org
http://matrix.skku.ac.kr/LA-Lab/Solution/
matrix.skku.ac.kr
[방사선이야기] #5 RI의 이용 : 의료분야에서의 활용2 CT — Steemit
안녕하세요!! @chosungyun입니다. 오늘은 저번 시간의 X-ray 촬영의 업그레이드 버전인 CT에 대해서 알아보려고 합니다. 저는 아직까지 CT를 찍어본 적이 한번밖에 없어서 실제로 본적은 한번뿐이지만
steemit.com
Impressive package for 3D and 4D graph - R software and data visualization - Easy Guides - Wiki - STHDA
Statistical tools for data analysis and visualization
www.sthda.com
'녕's Study > 선형대수학' 카테고리의 다른 글
| [k-mooc] 3.4 부분공간과 일차독립 (0) | 2022.02.09 |
|---|---|
| [k-mooc] 3.3 행렬대수_기본행렬 (0) | 2022.01.18 |
| [k-mooc] 3.2 행렬대수_역행렬 (0) | 2022.01.17 |
| [kmooc] 3.1 행렬대수 - 행렬연산 (0) | 2022.01.14 |
| [k-mooc] 1 벡터 (0) | 2021.12.31 |




