선형대수학은 "벡터(vector)", "행렬(matrix)"를 대상으로 연구함.
1.1 공학과 수학에서의 벡터
1.2 내적과 직교
1.3 직선과 평면의 벡터 방정식
1.1 공학과 수학에서의 벡터
물리학에서 벡터
운동법칙, 속도, 가속도, 힘 등을 나타내는데 쓰임
물리학적 힘의 구성은 전자기장 등의 다양한 벡터들의 공간을 나타내는데 쓰임
사회과학에서도 널리 쓰임
스칼라(scalar)
ex)길이, 넓이, 질량, 온도
크기가 주어지는 양적 값
벡터(vector)
ex) 속도, 위치이동, 힘
크기뿐만 아니라 방향까지 주어져야 표현할 수 있는 양적 값
즉, 크기와 방향을 갖는 유향선분
2차원, 3차원 공간의 벡터는 화살표로 표현할 수 있음.

영벡터
시작점과 끝점이 동일하여 크기가 0인 벡터
두 벡터의 합(vector sum)과 스칼라배(scalar multiplication)
두 벡터 x, y와 스칼라 k에 대하여, 두 벡터의 합 x+y와 스칼라배 kx에 대한 정의
1) x+ y는 평행사변형의 대각선으로 표시되는 벡터

2) kx는 k>0(양수)이면, x와 방향이 같고 길이는 k배하여 얻어지는 벡터임
k<0(음수)이면, x와 방향이 반대이고 길이는 \( \mid k \mid \)배하여 얻어지는 벡터임
k=0이면, 길이가 0인 벡터임
평면벡터(vector in the plane)
두 실수들의 순서조 \( (x_1, y_1) \)를 평면벡터라고 한다.
\( x = \left(x_{1},x_{2}\right) \)
\( x = \begin{bmatrix} x_{1} \\ y_{2} \end{bmatrix} \)
* 두 실수는 (평면)벡터 x의 성분(component)이다.
\( x = \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} , y = \begin{bmatrix} y_{1} \\ y_{2} \end{bmatrix} \)
* R²의 벡터 x = (x₁, x₂) , y = (y₁, y₂)에 대하여 x₁ = y₁ , x₂ = y₂이면 x = y라고 한다.
\( R^{2} = { \left({x}_{1},{x}_{2}\right)\mid{x}_{1},{x}_{2} \in R } \)
* 두 원소는 벡터 공간에 속한다.
\( \overset{\longrightarrow}{PQ} = \overset{\longrightarrow}{OQ^\prime} = \left(y_{1}-x_{1} , y_{2}-x_{2}\right) \)
* 시작점이 원점이 아닌 벡터의 경우, 시작점 P의 벡터에서 끝점 Q의 벡터를 뺀 성분을 가짐.

평면에서의 벡터합, 스칼라배, 영벡터, 음벡터
(vector sum, scalar multiplication, zero vector in the plane)
\( R^2\) 의 벡터 \( x = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}, y = \begin{bmatrix} y_1 \\ y_2 \end{bmatrix} \)와 스칼라 k에 대하여
\( x + y = \begin{bmatrix} x_1+y_1 \\ x_2+y_2 \end{bmatrix} \)
* 벡터의 합
\( x + (-1)x = 0 \)
*영벡터와 음벡터
[실습] 평면에서의 벡터합, 벡터차, 스칼라배
a=vector([1, 2])
b=vector([-2, 4])
# 벡터 생성, 형식은 a=vector([성분, 성분])
print "a=", a
print "b=", b
print
print "a+b=", a+b # 벡터의 합
print "a-b=", a-b # 벡터의 차
print "-2*a=", -2*a # 벡터의 스칼라배
공간벡터(vector in space)
세 실수들의 순서조(x₁, y₁, z₁)를 공간벡터라고 한다.
\( \overset{\longrightarrow}{PQ} = \overset{\longrightarrow}{OQ^\prime} = \left(y_{1}-x_{1} , y_{2}-x_{2}, y_{3}-x_{3}\right) \)
* 시작점이\( P(x_1, x_2, x_3) \), 끝점이 \( Q(y1, y2, y3) \) 인 유향성분의 벡터
n차원 벡터(n-dimensional vector)
n개 실수들의 순서조(x₁, x₂, ,x₃ ... , x_n)를 n차원 벡터라고 한다.
[실습] n차원에서 벡터합, 벡터차, 스칼라배
(vector sum, scalar multiplication)
a=vector([1, 2, -3, 4])
b=vector([-2, 4, 1, 0])
# 벡터 생성, 형식은 a=vector([성분, 성분, ..., 성분])
print "a=", a
print "b=", b
print
print "a+b=", a+b # 벡터의 합
print "a-b=", a-b # 벡터의 차
print "-2*a=", -2*a # 벡터의 스칼라배
n차원에서의 벡터 성질 1
Rⁿ의 벡터 x, y, z와 스칼라 h, k에 대하여 다음이 성립
* 덧셈 및 뺄셈은 순서, 괄호에 관계 없이 동일함
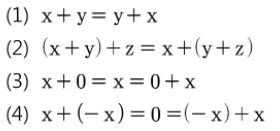
* 괄호 밖의 스칼라의 위치는 상관 없음
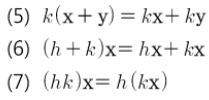
* 1을 곱하면 자기 자신
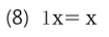
n차원에서의 벡터 성질 2
Rⁿ의 벡터 x와 스칼라 k에 대하여 다음이 성립
* 0을 곱하면 0임
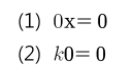
* 음수와 벡터를 곱하면 음벡터
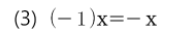
일차결합(linear combination)
\( v_1,v_2,v_3,..., v_k \)가 \( R^n \)의 벡터이고, 계수 \( c_1, c_2, c_3, ... , c_k \)가 실수일 때,
\( x = c_1 v_1 + c_2 v_2 + c_3 v_3 + ... + c_k v_k \)
의 형태를 \( v_1, v_2,..., v_k\)의 일차결합이라고 한다.
[실습] 벡터 a,b,c의 일차결합
a=vector([1, 2, -3, 4])
b=vector([-2, 4, 1, 0])
c=vector([5, -2, 3, -7])
print "a=", a
print "b=", b
print "c=", c
print
print "2*a-3*b+c=", 2*a-3*b+c # 일차결합
1.2 내적과 직교
노름, 거리(norm, distance)
\( \parallel \ x \ \parallel \ = \sqrt{x^2_1 + x^2_2 + x^2_3 + ...+ x^2_n} \)
* Rⁿ의 벡터 x(x₁, x₂, .... , x_n)에 대한 노름(norm, length, magnitude)임.
* 원점에서 P(x₁, x₂, .... , x_n)에 이르는 거리로 정의함.
\( \parallel \ x-y \ \parallel \ = \sqrt{ \left( x_1 - y_1 \right)^2 + \left( x_2 - y_2 \right)^2 + ...+ \left( x_n - y_n \right)^2} \)
* 두 점 P(x₁, x₂, .... , x_n)와 Q(y₁, y₂, .... , y_n)에 이르는 거리
[실습] 벡터의 노름, 거리 구하기
a=vector([2, -1, 3, 2])
b=vector([3, 2, 1, -4])
print "a=", a
print "b=", b
print
print "|a|=", a.norm() # 노름 계산, 형식은 a.norm()
print "|b|=", b.norm() # 노름 계산
print "|a-b|=", (a-b).norm() # 거리 계산
내적(Euclidean inner product, dot product)
\( x·y = x_1 y_1 + x_2 y_2 + ... + x_n + y_n \)
* Rⁿ의 벡터 x(x₁, x₂, .... , x_n)와 y(y₁, y₂, .... , y_n) 대한 내적(norm, length, magnitude)임.
* 내적은 x·y로 표시함.
같은 벡터의 내적
\( x·x \ = \ x_1 x_1 + x_2 x_2 + ... + x_n x_n = x^2_1 + x^2_2 + ... + x^2_n \ = \ \parallel x \parallel ^2 \)
[실습] 두 벡터의 내적
a=vector([2, -1, 3, 2])
b=vector([3, 2, 1, -4])
print "a=", a
print "b=", b
print
print a.inner_product(b)
# 내적 계산, 형식은 a.inner_product(b)
내적의 성질
Rⁿ의 벡터 x, y, z와 스칼라 k에 대하여 다음이 성립
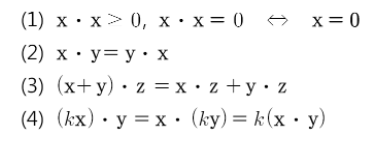
코시-슈바르츠 부등식(Cauchy-Schwarz inequality)


Rⁿ의 임의의 벡터 x, y에 대하여 다음이 성립
\( \mid x·y \mid \le \parallel x \parallel \parallel y \parallel \)
* x와 y의 내적에 대한 절대값이 x와 y 각각의 노름의 곱보다 작거나 같다.
두 벡터 사이의 각(angle)
\( x·y = \parallel x \parallel \parallel y \parallel \ cos \theta \qquad \left( 0 < \theta < \pi \right) \)
* θ는 x와 y가 이루는각(angle, 사잇각)
직교와 평행
x와 y의 내적이 0일 때, x와 y는 서로 직교한다.
= 두 벡터 x와 y의 사잇각이 직각이면 직각임.
적당한 실수 k에 대하여 x = ky인 경우, x는 y와 평행한다.
= x가 y의 스칼라 배이면 평행임.
단위벡터, 직교벡터, 정규직교벡터
(unit vector, orthogonal vector, orthonormal vector)
\( \parallel x \parallel = 1 \)
* Rⁿ의 벡터 x에 대하여 노름이 1인 경우, 단위벡터(unit vector)라고 함.
\( \mid x · y \mid = 0 \)
* Rⁿ의 벡터 x, y가 직교이면, 직교벡터(orthogonal vector)라고 함.
* x와 y가 직교벡터이면서 각각 단위벡터이면 정규직교벡터(orthonormal vector)라고 함.
[실습] 두 벡터의 내적
a=vector([1, 0, 1, 1])
b=vector([-1, 0, 0, 1])
print "a=", a
print "b=", b
print
print a.inner_product(b)
벡터에 대한 삼각부등식(triangle inequality)
\( \parallel x + x \parallel \ \le \ \parallel x \parallel + \parallel y \parallel \)

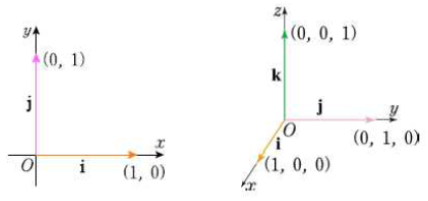
기본단위벡터(standard unit vector)
\( u = \frac{1}{ \parallel X \parallel } X \)
* 임의의 벡터 X(≠0)에 대한 단위벡터라고 함.
\( e_1 = (1,0,0,...,0) \)
\( e_2 = (0,1,0,...,0) \)
\( ... \)
\( e_n = (0,0,0,...,1) \)
* Rⁿ의 단위벡터 중 n개의 벡터를 기본단위벡터(standard unit vector, 표준단위벡터)라고 함.
기본단위벡터와 임의의 벡터
\( X = x_1 e_1 + x_2 e_2 +....+ x_n e_n \)
1.3 직선과 평면의 벡터 방정식
직선의 방정식 (기울기(방향벡터)와 한 점)
\( R^3 \)에서 직선 \(l\)은 한 점 \( P_0 \left( x_0, y_0, z_0 \right) \)를 지나고 0이 아닌 벡터 \( a = ai + bj + ck \)에 평행함.
벡터 \(a\)와 \( \overset{ \longrightarrow }{ P_0 P } \)가 평행함. 즉, \( \overset{ \longrightarrow }{ P_0 P } = ta \), \( ( t \in R ) \)를 만족하는 점 \( P(x,y,z) \) 전체의 집합과 같다.
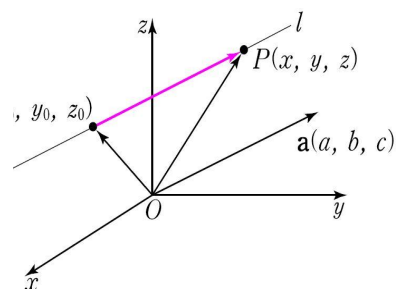
\( P = P_0 + ta, \left( p = \overset{ \longrightarrow }{ OP }, p_0 = \overset{ \longrightarrow }{ OP_0 } \right) \)
* 벡터방정식
* 점 \( P(x,y,z) \)에 대하여 정리
\( x = x_0 + ta, \ y = y_0 + tb, z = z_0 + tc, \left( - \infty < t < \infty \right) \)
* 직선의 매개변수 방정식
* 각 매개변수 \( x , y , z \)에 대하여 정리
\( \frac{ x - x_0}{ a } = \frac{ y - y_0 }{ b } = \frac{ z - z_0 }{ c } \left( = t \right) , \left( a, b, c \ne 0 \right) \)
* 직선의 대칭방정식
* t(스칼라배)에 대하여 매개변수 방정식을 정리
직선의 방정식 1
점 \( P(2, -1, 3) \)을 지나고 벡터 \( a= (-3. 2. 4) \)에 평행한 직선의 방정식은 다음과 같이 표현할 수 있음.
(1)
\( xi + yi + zk = 2i -j + 3k + \left( -3i + 2j + 4k \right) t \)
(2)
\( \begin{cases} x=2-3t \\ y=-1+2t \ \left( - \infty < t < \infty \right) \\ \vdots \\ =4+4t \end{cases} \)
(3)
\( \frac{x-2}{-3} = \frac{y+1}{2} = \frac{z-3}{4} \)
직선의 방정식 2
Q) 두 점 \( P \left( -1,2,4 \rignt), Q \left( 2,0,-1 \right)을 지나는 직선의 매개(변수) 방정식을 구하라.
A)
- 1) 직선에 평행한 0이 아닌 벡터(내적) 구하기
\( \overset{ \longrightarrow }{ PQ } = ((-1 - 2), (2 - 0), (4 - -1)) = (-3, 2, 5) \) - 2) 점 \( P \)를 지나고 벡터와 평행하는 매개변수 구하기
\( x= -1 -3t, y = -2 -2t, z=4-5t \ (- \infty < t < \infty ) \)
평면의 방정식 (point-noraml 방정식, 법선벡터(normal vector)와 한 점)
\( R^3 \)에서 한 점 \(P_0(x_0, y_0, z_0) \)를 지나고 0 아닌 벡터를 \( n=(A,B,C) \) 법선벡터라고 함.
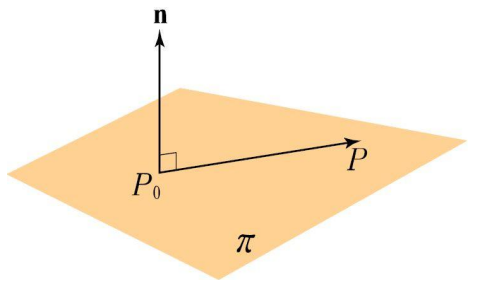
\( n · \overset{ \longrightarrow }{ P_0P } = (A,B,C) · (x-x_0, y-y_0, z-z_0)=0 \)
* 법선벡터에 수직인 벡터들이 이루는 평면\( \pi \)
\( ax + by + cz + d = 0 \)
* 일반적인 평면의 방정식
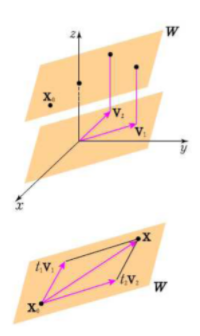
\( x = x_0 + t_1 v_1 + t_2 v_2 \ , \ ( - \infty < t_1, t_2 < \infty ) \)
* 평면의 벡터방정식
\( \begin{align} & x_0 = (x_0,y_0,z_0), \\ & v_1 = (a_1,b_1,c_1), \\ & v_2 = (a_2, b_2, c_2) \end{align} \)
\( \begin{align} & x=x_0 + a_1 t_1 + a_2 t_2, \\ & y = y_0 + b_1 t_1 + b_2 t_2, \\ & z=z_0 + c_1 t_1 + c_2 t_2 \end{align} \)
* 평면의 매개변수 방정식
[실습] 평면의 방정식
Q) 세 점 \( P(4,-3,1), \ Q(6,-4,7), R(1,2,2) \)를 지나는 평면의 벡터방정식과 매개(변수) 방정식을 구하라.
A)
- 한 점 \( P(4,-3,1) \)과 두 벡터 \(Q, \ R \)의 벡터방정식
\( x_1 - x_0 = \overset{ \longrightarrow }{ PQ } = ((6-4),(-4+3),(7-1)) = (2,-1,6) \)
\( x_2 - x_0 = \overset{ \longrightarrow }{ PR } = ((1-4),(2+3),(2-1)) = (-3,5,1) \)
\( P = x_0 + (2,-1,6)t_1 + (-3,5,1)t_2 \) - 한 점 \( P(4,-3,1) \)의 각 매개변수에 대한 방정식
\( \begin{align} & x = 4 + 2t_1 -3t_2 \\ & y = -3 -t_1 + 5t_2 \ ( - \infty < t_1, t_2 < \infty) \\ & z = 1 + 6t_1 + t_2 \end{align} \)
var('t,x,y,z,P_1,Q_1,R_1,P_2,Q_2,R_2,P_3,Q_3,R_3')
@interact
def _(p1=input_box(vector([4,-3,1]), label="$P$", type=vector),p2=input_box(vector([6,-4,7]), label="$Q$", type=vector),p3=input_box(vector([1,2,2]), label="$R$", type=vector), auto_update=false ):
A=matrix(4,4,[1,x,y,z,1,p1[0],p1[1],p1[2],1,p2[0],p2[1],p2[2],1,p3[0],p3[1],p3[2]])
A1=matrix(3,3,[p1[0],p1[1],p1[2],p2[0],p2[1],p2[2],p3[0],p3[1],p3[2]])
A2=matrix(3,3,[1,p1[1],p1[2],1,p2[1],p2[2],1,p3[1],p3[2]])
A3=matrix(3,3,[1,p1[0],p1[2],1,p2[0],p2[2],1,p3[0],p3[2]])
A4=matrix(3,3,[1,p1[0],p1[1],1,p2[0],p2[1],1,p3[0],p3[1]])
aa=A.det(); a1=A1.det(); a2=A2.det(); a3=A3.det(); a4=A4.det()
f=a1-a2*x+a3*y-a4*z
RRR=matrix(4,4,[1,x,y,z,1,P_1,Q_1,R_1,1,P_2,Q_2,R_2,1,P_3,Q_3,R_3])
ma=[]; mi=[]; PP=[p1,p2,p3]
for i in srange(0,3,1):
ma += [max(p1[i],p2[i],p3[i])]; mi += [min(p1[i],p2[i],p3[i])]
try:
D= A.inverse()
P = implicit_plot3d(f==0, (x,mi[0]-1,ma[0]+1),(y,mi[1]-1,ma[1]+1),(z,mi[2]-1,ma[2]+1), opacity=0.2,color="red")
for i in srange(0,3,1):
P += point3d([PP[i]],size=10)
P += text3d(vector(PP[i]),vector(PP[i])-vector([0,0,0.3]))
TT ='det$%s =0$'%(latex(RRR))
TT +='<p>$\Rightarrow %s =0$'%(latex(f))
html.table([[TT]])
P.show(spin='true')
except:
html( '$P_1,P_2,P_3$ are collinear.$')
정사영(projection)
\( R^3 \)에 벡터 \( x = \overset{ \longrightarrow }{ OQ } \)와 \(y = \overset{ \longrightarrow }{ OP } \)가 있고 \( x \ne 0 \)이며, 점 \( P \)에서 \( OQ \)에 내린 수선의 발을 \( S \)라고 할 때,
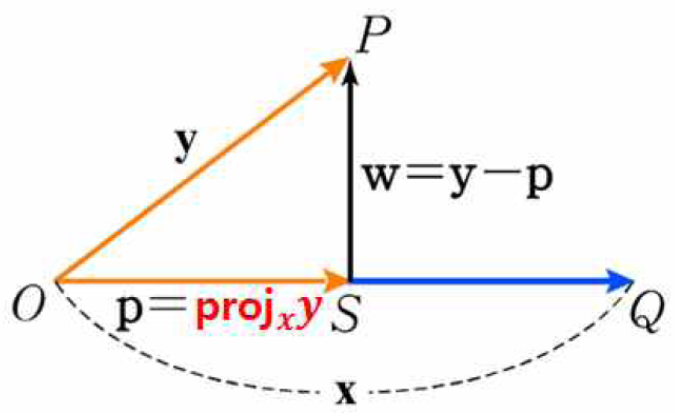
벡터 \( p = \overset{ \longrightarrow }{ OS } \)를 \( x \) 위로의 \( y \)의 정사역이라고 하며 \( proj_x y \)로 나타냄.
이때 벡터 \( w = \overset{ \longrightarrow }{ SP } \)를 \( x \)에 수직인 \( y \)의 벡터성분(vector component)이라 함.
\( R^3 \)의 벡터 \( x( \ne 0), \ y\)에 대하여 다음이 성립함.
\( proj_x y \ = \ tx \ = \ \frac{ (y \ · \ x) }{ x \ · \ x } x \)
\( D = \parallel proj_x y \parallel = \frac{ \mid y \ · \ x \mid }{ \parallel x \parallel } \)
[실습] 정사영과 벡터 구하기
Q) \( x=(2,-1,3), \ y=(4,-1,2) \)에 대하여 \( x \) 위로의 \( y \)의 정사영 \( proj_x y \)와 \( x \)에 수직인 \( y \) 벡터성분 \( w \)를 구하라.
a)
- 정사영
\( proj_x y \ = \ \frac{ (2 \times 4) + (-1 \times -1) + (3 \times 2) }{ (2)^2 + (-1)^2 + (3)^2 } (2, -1, 3) \) - 벡터 w
\( w = y - proj_x y = (4,-1,2) - ( \frac{15}{7}, \frac{-15}{14}, \frac{45}{14} ) = ( \frac{13}{7}, \frac{1}{14}, \frac{-17}{14} \)
x=vector([2, -1, 3])
y=vector([4, -1, 2])
yx=y.inner_product(x)
xx=x.inner_product(x)
p=yx/xx*x
w=y-p
print "x=", x
print "y=", y
print
print "p=", p
print "w=", w
점과 평면 사이의 거리
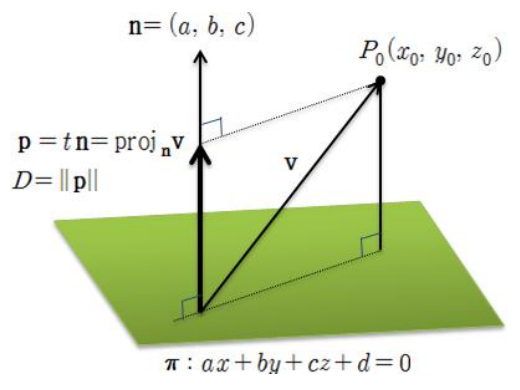
\( D = \frac{ \ \mid ax_0 \ + \ by_0 \ + \ cz_0 \ + \ d \ \mid }{ \sqrt{ a^2 \ + \ b^2 \ + \ c^2 } } \)
* 점 \( P_0(x_0, y_0, z_0) \)와 평면 \( \pi : ax + by + d = 0 \) 사이의 거리 D
점과 평면 사이의 거리(D) 구하기
Q) 점 \( P(3,-1,2) \)에서 평면 \( x + 3y -2z -6 = 0 \)에 이르는 거리 \( D \)를 구하라.
A)
\( D = \frac{ (1 \times 3) + (3 \times -1) + (-2 \times 2) + (-6) }{ \sqrt{ 1^2 + 3^2 + (-2)^2}} \)
참고
위키백과:TeX 문법 - 위키백과, 우리 모두의 백과사전
이 문서는 한국어 위키백과의 정보문입니다.이 문서는 정책과 지침은 아니지만, 위키백과의 규범과 관습 측면에서 공동체의 확립된 관행을 설명하고 있습니다. 공동체의 총의나 검토를 어느 정
ko.wikipedia.org
http://matrix.skku.ac.kr/K-MOOC-LA/LA-Book.pdf
'녕's Study > 선형대수학' 카테고리의 다른 글
| [k-mooc] 3.4 부분공간과 일차독립 (0) | 2022.02.09 |
|---|---|
| [k-mooc] 3.3 행렬대수_기본행렬 (0) | 2022.01.18 |
| [k-mooc] 3.2 행렬대수_역행렬 (0) | 2022.01.17 |
| [kmooc] 3.1 행렬대수 - 행렬연산 (0) | 2022.01.14 |
| [k-mooc] 2 선형연립방정식 (0) | 2022.01.05 |




