k-mooc 으로 선형대수학 독학하기 !
강의 내용 : 선형대수학
출처 : 성균관대학교 이상구 교수님
* 원래 강의는 sage를 이용하는데 중간부터 나는 R을 사용하는 것으로 변경함.
부분공간(Subspace)
집합 \( W(\ne \phi) \)가 \( R^n \)의 부분집합일 때,
( 집합 \( W \)가 공집합이 아니고 n차원 집합의 부분집합일 때)
다음 두 조건을 만족하면 \( W \)는 \( R^n \)의 부분공간임.
1) \( x, y \in W \Rightarrow x + y \in W \) (벡터덧셈에 닫혀있다.)
2) \( x \in W, k \in R \Rightarrow kx \in W \) (스칼라배에 닫혀있다.)
comment : 닫혀있다...? 속한다..?인가
* \( R^n \)의 모든 부분공간은 영벡터를 포함해야 한다.
\( x \in W, 0 \in R \Rightarrow 0x = 0 \in W \)
부분공간 1
\( \{ 0 \} \)과 \( R^n \)는 \( R^n \)의 부분공간임. 여기서 \( 0 = (0, \cdots, 0) \)은 원점임.
부분공간 2
\( L_0 = \{(x,y) \in R^2 \mid y = x \} \)
* 직선 \( y = x \) 위의 점들의 집합
* 위의 두 조건을 만족하므로 \( R^2 \)의 부분공간임.
\( L_1 = \{ (x,y) \in R^2 \mid y = x + 1 \} \)
* 직선 \( y = x +1 \) 위의 점들의 집합
* \( (0,1), (1,2) \in L_1 \)이지만 \( (0,1) + (1,2) = (1,3) \in L_1 \) (벡터덧셈에 닫혀있지 않음)
* 따라서 직선 \( y = x + 1 \)위의 점들의 집합은 부분공간의 조건을 만족하지 못하므로 \( R^2 \)의 부분공간이 아님.
부분공간 3
다음 중 하나는 \( R^2 \)의 부분공간임. (2차원의 부분공간)
1) 영공간 : \( \{0 \} \)
2) 원점을 지나는 직선
3) \( R^2 \) 전체
다음 중 하나는 \( R^3 \)의 부분공간임. (3차원의 부분공간)
1) 영공간 : \( \{0 \} \)
2) 원점을 지나는 직선
3) 원점을 지나는 평면
4) \( R^3 \) 전체
[문제] 부분공간 4
집합 \( W = \{ (0,a,b,c,d,0) \mid a,b,c,d in R \} \)은 \( R^6 \)의 부분공간임을 나타내라
\( \begin{align} & (1) \ x + y = (0, \ a_1+a_2, \ b_1 + b_2, \ c_1 + c_2, \ d_1 + d_2, \ 0) \\ & (2) \ kx = (0, \ ka_1, \ kb_1, \ kc_1, \ kd_1, \ 0) \\ & \therefore \ x+y \in W, \ kx \in W \end{align} \)
* 임의의 \( x = (0,a_1,b_1,c_1,d_1,0), y=(0,a_2,b_2,c_2,d_2,0) \in W, k \in R \)에 대하여 조건이 성립함.
* 따라서 \( W \)는 \( R^6 \)의 부분공간임.
[문제] 부분 공간 5
행렬 \( A = [a_{ij}]_{m \times n} \)에 대하여 \( W = \{ x \in R^n \mid Ax = 0 \} \)는 벡터공간 \( R^n \)의 부분공감임을 나타내라.
(이러한 \( W \)를 \( Ax = 0 \)의 해공간(Solution Space) 또는 \( A \)의 영공간(Null Space)라고 함.
\( \begin{align} & A(x + y) = Ax + Ay = 0 + 0 = 0 \\ & A(kx) = k(Ax) = k0 = 0 \\ & \therefore \ x + y \in W, kx \in W \end{align} \)
* \( A0 = 0 \)이므로 \( 0 \in W \), 즉 \( W \ne \phi \)임.
( \( A \times 0 = 0 \)이므로 \( 0 \)은 \( W \)의 부분집함임. 따라서 집합 \( W \)는 공집합이 아닌 것임. )
* \( x, y \in W \)와 \( k \in R \)에 대하여 \( Ax = 0, Ay = 0 \)임.
* 따라서 \( W \)는 \( R^n \)의 부분공간임.
일차 결합(Linear Combination)
\( x = c_1x_1 + c_2x_2 + \cdots + c_kx_k, \qquad c_1,c_2, \cdots , c_k \in R \)
* \( R^n \)의 부분집합 \( \{ x_1, x_2, \cdots , x_k \} \)에 대하여, \( x \in R^n \)의 형태가 위와 같을 때
* \( x \)를 벡터 \( x_1, x_2, \cdots , x_k \)의 일차결합이라고 함.
[문제] 일차 결합 1
\( R^3 \)의 벡터 \( x_1 = (1,-2,-1), x_2 = (3, -5, 4) \)에 대하여 \( x=(2,-6,3) \)을 \( x_1,x_2 \)의 일차결합으로 표시할 수 있는가?
\( x = c_1x_1 + c_2x_2 \)
* 위의 일차결합을 만족하는 실수 \( c_1, c_2 \)의 존재 여부에 의해 결정됨.

* 위의 일차방정식을 만족하는 실수 \( c_1, c_2 \)는 존재하지 않음.
* 벡터 \( x \)는 \( x_1, x_2 \)의 일차결합으로 표시할 수 없음.
[문제] 일차 결합 2
\( W = \{ c_1x_1 + c_2x_2 + \cdots + c_kx_k \mid c_1, c_2, \cdots , c_k \in R \} \)
* \( R^n \)의 부분집합 \( S = \{ x_1, x_2, \cdots , x_k \} \)에 대하여 \( S \)에 있는 \( k \)개 벡터들의 일차결합 전체의 집합인 \( W \)가 \( R^n \)의 부분공감임을 보여라.

* \( x, y \in W , k \in R \)이면, \( C_i, d_i \in R \\( i = 1,2, \cdots , k) \)에 대하여 위와 같이 쓸 수 있음.
\( \begin{align} & x + y = (c_1 + d_1)x_1 + (c_2 + d_2)x_2 + \cdots + (c_k + d_k)x_k, \\ & kx = (kc_1)x_1 + (kc_2)x_2 + \cdots + (kc_k)x_k \\ & \therefore x+ y = \in W, kx \in W \end{align} \)
* \( W \)는 \( R^n \)의 부분공간임.
생성(Span), 생성 집합(Spanning Set)
\( W = \{ c_1x_1 + c_2x_2 + \cdots + c_kx_k \mid c_1, c_2, \cdots , c_k \in R \} \)
* \( R^n \)의 부분집합 \( S = \{x_1, x_2, \cdots , x_k \} \)에 대하여 \( S \)에 있는 \( k \)개 벡터들의 일차결합 전체의 집합
* \( S \)에 의하여 생성된(Spanned) \( R^n \)의 부분공간
\( W = span(S) = < S > \)
* 집합 \( S \)는 \( W \)를 생성(Span)한다고 함.
* \( S \)를 \( W \)의 생성집합(Spanning Set)이라고 함.
\( \begin{align} & R^n = <S> \\ & \quad = \{ c_1x_1 + c_2x_2 + \cdots + c_kx_k \mid c_1, c_2, \cdots , c_k \in R \} \end{align} \)
* 특히 \( R^n \)에 있는 모든 벡터가 \( S \)에 있는 \( k \)개 벡터들의 일차결합이면 집합 \( S \)는 \( R^n \)을 생성함.
열공간(Column Space), 행공간(Row Space)
\( < A^{(1)}, A^{(2)}, \cdots , A^{(n)} > \) 또는 \( Col(A) \)
* \( A =[a_{ij}] \in M_{m \times n} \)이면 \( A \)의 열벡터들 \( A^{(1)}, A^{(2)}, \cdots , A^{(n)} \)의 생성(Span)의 \( R^m \)의 부분공간임.
* 행렬 \( A \)의 열공간(Column Space)라고 함.
\( < A_{(1)}, A_{(2)}, \cdots , A_{(n)} > \) 또는 \( Row(A) \)
* \( A \)의 행벡터들은 \( R^n \)의 부분공간임.
* 행렬 \( A \)의 행공간(Row Space)라고 함.
[R 실습] 열공간과 행공간
library(matlib)
x1 <- c(1,0,1)
x2 <- c(-3,1,1)
x3 <- c(-2,1,2)
x <- cbind(x1,x2,x3)
A <- matrix(x, ncol=3, nrow=3, byrow=T)
B <- echelon(A,verbose=TRUE, fractions=TRUE) # RREF

일차독립(linearly independent), 일차종속(linearly dependent)

* \( S = { x_1, x_2, \cdots , x_k } \subseteq R^n \)에 대하여 위와 같으면,
* 벡터 \( { x_1, x_2, \cdots , x_k } \)(or 집합 S)는 일차독립(linearly independent)라고 함.
* 벡터 \( { x_1, x_2, \cdots , x_k } \)(or 집합 S)가 일차독립이 아니면, 일차종속(linearly dependent)라고 함.
* 집합 \( S \)가 일차종속이면, \( c_1x_1 + c_2x_2 + \cdots + c_kx_k = 0 \)을 만족하는 모두는 영이 아닌 스칼라 \( c_1, c_2, \cdots , c_k \)가 존재함.
comment) 스칼라 \( c_1, c_2, \cdots , c_k \)가 0이면 일차 독립, 0이 아니면 일차 종속임.
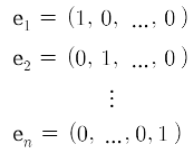
* 일반적으로, \( R^n \)의 기본 단위벡터 \( e_n \)에 대하여 \( S = {e_1, e_2, \cdots , e_n } \)은 일차독립임.
즉, \( n \)차원 공간에 존재하는 기본 단위벡터의 집합은 일차독립임.
* 다음과 같기 때문임.

일차독립과 일차종속 1
Q)

A)

* \( 2c_1 + c_2 = 0 \therefore c_1 = c_2 = 0 \)
* \( -c_1 + 3c_2 = 0 \therefore c_1 = c_2 = 0 \)
일차독립과 일차종속 2
Q)

A)

[R 실습] 일차독립과 일차종속 3
Q)

A)


library(matlib)
x1 <- c(1,0,-1)
x2 <- c(1,1,0)
x3 <- c(0,1,1)
x <- cbind(x1,x2,x3)
A <- matrix(x, ncol=3, nrow=3, byrow=T)
B <- echelon(A,verbose=TRUE, fractions=TRUE)
일차독립과 일차종속의 정리 1
\( S = \{ x_1, x_2, \cdots , x_k \} \subseteq R^n \)
* 집합 \( S \) : n차원의 \( R \)공간에 있는 벡터 \( x \)의 집합
* 집합 \( S \)가 일차종속이 되기 위한 필요충분조건 : \( S \)에 속하는 한 벡터가 나머지 벡터들의 일차결합으로 표시되어야 함.
* 집합 \( S \)가 영벡터를 포함하면 \( S \)는 일차종속임.
* 집합 \( S \)의 부분집합 \( S' \)이 일차종속이면 \( S \)도 일차종속이고, \( S \)가 일차독립이면 \( S' \)도 일차독립임.
* 즉, "벡터의 집합 \( S \)가 일차독립"은 \( S \)안의 어떤 벡터도 다른 벡터들의 일차결합으로 표시될 수 없으며,
모두가 꼭 필요한 벡터들이라는 의미임.
그리고, \( R^n \)에서 일차독립인 집합은 \( n \)개의 벡터들로 이루어져 있음.
증명
집합 \( S \)가 일차종속이면 다음을 만족하는 모두는 영이 아닌 스칼라 \( c_1, c_2, \cdots , c_k \)가 존재함.
\( c_1x_1 + x_2x_2 + \cdots + c_kx_k = 0 \)
일반성을 잃지 않고 \( c_1 \ne 0 \)라고 하면 다음과 같으므로 \( x_1 \)은 \( S \)에 속하는 나머지 벡터들의 일차결합으로 표시됨.
\( x_1 = ( \frac{-c_2}{c_1} ) x_2 + \cdots + ( \frac{-c_k}{c_1} )x_k \)
* \( c_1 x_1 \) 을 제외하고 모두 부등호 옆으로 넘김
* \( c_1 \)으로 모든 식을 나눔
일반성을 잃지 않고 \( x_1 = c_2x_2 + \cdots + c_kx_k \)라 하면 다음과 같으므로 \( -1 \ne 0 \)이므로 \( S \)는 일차종속임.
\( (-1)x_2 + c_2x_2 + \cdots + c_k x_k = 0 \)
comment) \( c_1= -1 \)이 라고 가정하고 증명한거임?
만약 \( x_1 = 0 \)이라 하면 임의의 영 아닌 스칼라 \( c_1 ( \ne ) 0 \)에 대하여 다음과 같으므로 \( S = {x_1 =0, x_2, \cdots , x_k } \)는 일차종속임.
\( c_1 0 + 0x_2 + \cdots + 0x_k = 0 \)
\( S \)의 부분집합 \( S' \)을 다음과 같다고 하고 \( S' \)이 일차종속이라 할 때
\( S' = {x_1, x_2, \cdots, x_h} , 2 \le h \le k \)
어떤 \( c_i \ne 0 (1 \le i \le h ) \)에 대하여 다음을 만족함.
\( c_1x_1 + \cdots + c_ix_i + \cdots + c_hx_h = 0 \)
따라서 다음과 같으므로 \( S \)는 일차종속임.
\( c_1x_1 + \cdots + c_ix_i + \cdots + c_hx_h + 0x_h+1 \cdots 0x_k = 0 \)
* 또한 이 명제의 대우도 참이므로, \( S \)가 일차독립이면 \( S' )\도 일차독립임.
일차독립과 일차종속의 정리 2
\( R^n \)에서 \( m (>n) \)개의 벡터는 항상 일차종속임.
= n차원의 R공간에서 벡터의 수가 n차원의 개수 보다 많으면 일차종속임.
ex) \( R^3 \)의 벡터 \( x_1 = (1,0,0), x_2 = (1,1,0), x_3 = (1,1,1), x_4 =(0,1,1) \)에 대하여 \( S = {x_1,x_2,x_3,x_4}는
\( m = 4, \quad n= 3 \)이므로 일차종속임.
'녕's Study > 선형대수학' 카테고리의 다른 글
| [k-mooc] 3.3 행렬대수_기본행렬 (0) | 2022.01.18 |
|---|---|
| [k-mooc] 3.2 행렬대수_역행렬 (0) | 2022.01.17 |
| [kmooc] 3.1 행렬대수 - 행렬연산 (0) | 2022.01.14 |
| [k-mooc] 2 선형연립방정식 (0) | 2022.01.05 |
| [k-mooc] 1 벡터 (0) | 2021.12.31 |




